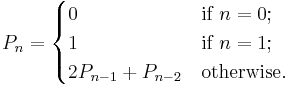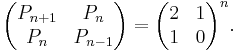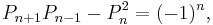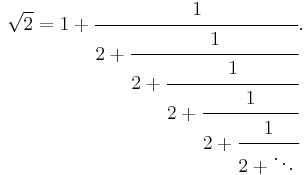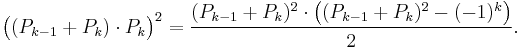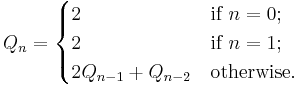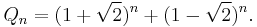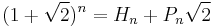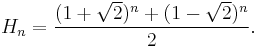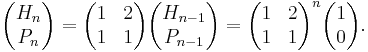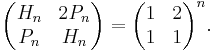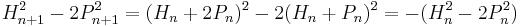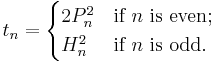Pell number

In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell-Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82.

Both the Pell numbers and the companion Pell numbers may be calculated by means of a recurrence relation similar to that for the Fibonacci numbers, and both sequences of numbers grow exponentially, proportionally to powers of the silver ratio 1 + √2. As well as being used to approximate the square root of two, Pell numbers can be used to find square triangular numbers, to construct integer approximations to the right isosceles triangle, and to solve certain combinatorial enumeration problems.[1]

As with Pell's equation, the name of the Pell numbers stems from Leonhard Euler's mistaken attribution of the equation and the numbers derived from it to John Pell. The Pell-Lucas numbers are also named after Édouard Lucas, who studied sequences defined by recurrences of this type; the Pell and companion Pell numbers are Lucas sequences.

Contents

Pell numbers

The Pell numbers are defined by the recurrence relation

P_n=\begin{cases}0&\mbox{if }n=0;\\1&\mbox{if }n=1;\\2P_{n-1}%2BP_{n-2}&\mbox{otherwise.}\end{cases}

In words, the sequence of Pell numbers starts with 0 and 1, and then each Pell number is the sum of twice the previous Pell number and the Pell number before that. The first few terms of the sequence are

0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378... (sequence A000129 in OEIS).

The Pell numbers can also be expressed by the closed form formula

P_n=\frac{(1%2B\sqrt2)^n-(1-\sqrt2)^n}{2\sqrt2}.

For large values of n, the \scriptstyle (1%2B\sqrt 2)^n term dominates this expression, so the Pell numbers are approximately proportional to powers of the silver ratio \scriptstyle (1%2B\sqrt 2), analogous to the growth rate of Fibonacci numbers as powers of the golden ratio.

A third definition is possible, from the matrix formula

\begin{pmatrix} P_{n%2B1} & P_n \\ P_n & P_{n-1} \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 0 \end{pmatrix}^n.

Many identities can be derived or proven from these definitions; for instance an identity analogous to Cassini's identity for Fibonacci numbers,

P_{n%2B1}P_{n-1}-P_n^2 = (-1)^n,

is an immediate consequence of the matrix formula (found by considering the determinants of the matrices on the left and right sides of the matrix formula).[2]

Approximation to the square root of two

Pell numbers arise historically and most notably in the rational approximation to the square root of 2. If two large integers x and y form a solution to the Pell equation

\displaystyle x^2-2y^2=\pm 1,

then their ratio 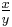\tfrac{x}{y} provides a close approximation to 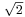\scriptstyle\sqrt 2. The sequence of approximations of this form is

1, \frac32, \frac75, \frac{17}{12}, \frac{41}{29}, \frac{99}{70}, \dots

where the denominator of each fraction is a Pell number and the numerator is the sum of a Pell number and its predecessor in the sequence. That is, the solutions have the form 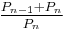\tfrac{P_{n-1}%2BP_n}{P_n}. The approximation

\sqrt 2\approx\frac{577}{408}

of this type was known to Indian mathematicians in the third or fourth century B.C.[3] The Greek mathematicians of the fifth century B.C. also knew of this sequence of approximations;[4] they called the denominators and numerators of this sequence side and diameter numbers and the numerators were also known as rational diagonals or rational diameters.[5]

These approximations can be derived from the continued fraction expansion of 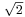\scriptstyle\sqrt 2:

\sqrt 2 = 1 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \ddots\,}}}}}.

Truncating this expansion to any number of terms produces one of the Pell-number-based approximations in this sequence; for instance,

\frac{577}{408} = 1 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2 %2B \cfrac{1}{2}}}}}}}.

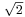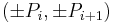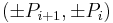As Knuth (1994) describes, the fact that Pell numbers approximate \scriptstyle\sqrt 2 allows them to be used for accurate rational approximations to a regular octagon with vertex coordinates (\pm P_i,\pm P_{i%2B1}) and (\pm P_{i%2B1},\pm P_i). All vertices are equally distant from the origin, and form nearly uniform angles around the origin. 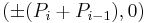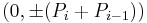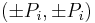Alternatively, the points (\pm(P_i%2BP_{i-1}),0), (0,\pm(P_i%2BP_{i-1})), and (\pm P_i,\pm P_i) form approximate octagons in which the vertices are nearly equally distant from the origin and form uniform angles.

Primes and squares

A Pell prime is a Pell number that is prime. The first few Pell primes are

2, 5, 29, 5741, ... (sequence A086383 in OEIS).

As with the Fibonacci numbers, a Pell number 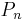P_n can only be prime if n itself is prime.

The only Pell numbers that are squares, cubes, or any higher power of an integer are 0, 1, and 169 = 132.[6]

However, despite having so few squares or other powers, Pell numbers have a close connection to square triangular numbers.[7] Specifically, these numbers arise from the following identity of Pell numbers:

\bigl((P_{k-1}%2BP_k)\cdot P_k\bigr)^2 = \frac{(P_{k-1}%2BP_k)^2\cdot\left((P_{k-1}%2BP_k)^2-(-1)^k\right)}{2}.

The left side of this identity describes a square number, while the right side describes a triangular number, so the result is a square triangular number.

Santana and Diaz-Barrero (2006) prove another identity relating Pell numbers to squares and showing that the sum of the Pell numbers up to 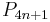P_{4n%2B1} is always a square:

\sum_{i=0}^{4n%2B1} P_i = \left(\sum_{r=0}^n 2^r{2n%2B1\choose 2r}\right)^2 = (P_{2n}%2BP_{2n%2B1})^2.

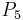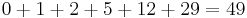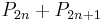For instance, the sum of the Pell numbers up to P_5, 0%2B1%2B2%2B5%2B12%2B29=49, is the square of P_2%2BP_3=2%2B5=7. The numbers P_{2n}%2BP_{2n%2B1} forming the square roots of these sums,

1, 7, 41, 239, 1393, 8119, 47321, ... (sequence A002315 in OEIS),

are known as the Newman–Shanks–Williams (NSW) numbers.

Pythagorean triples

If a right triangle has integer side lengths a, b, c (necessarily satisfying the Pythagorean theorem a2+b2=c2), then (a,b,c) is known as a Pythagorean triple. As Martin (1875) describes, the Pell numbers can be used to form Pythagorean triples in which a and b are one unit apart, corresponding to right triangles that are nearly isosceles. Each such triple has the form

(2P_{n}P_{n%2B1}, P_{n%2B1}^2 - P_{n}^2, P_{n%2B1}^2 %2B P_{n}^2=P_{2n%2B1}).

The sequence of Pythagorean triples formed in this way is

(4,3,5), (20,21,29), (120,119,169), (696,697,985), ....

Pell-Lucas numbers

The companion Pell numbers or Pell-Lucas numbers are defined by the recurrence relation

Q_n=\begin{cases}2&\mbox{if }n=0;\\2&\mbox{if }n=1;\\2Q_{n-1}%2BQ_{n-2}&\mbox{otherwise.}\end{cases}

In words: the first two numbers in the sequence are both 2, and each successive number is formed by adding twice the previous Pell-Lucas number to the Pell-Lucas number before that, or equivalently, by adding the next Pell number to the previous Pell number: thus, 82 is the companion to 29, and 82 = 2 * 34 + 14 = 70 + 12. The first few terms of the sequence are (sequence A002203 in OEIS): 2, 2, 6, 14, 34, 82, 198, 478...

The companion Pell numbers can be expressed by the closed form formula

Q_n=(1%2B\sqrt 2)^n%2B(1-\sqrt 2)^n.

These numbers are all even; each such number is twice the numerator in one of the rational approximations to 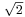\scriptstyle\sqrt 2 discussed above.

Computations and connections

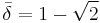The following table gives the first few powers of the silver ratio \delta=\delta_S=1%2B\sqrt2 and its conjugate \bar{\delta}=1-\sqrt{2}.

n (1%2B\sqrt{2})^n (1-\sqrt{2})^n
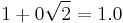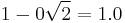0 1%2B0\sqrt{2}=1.0 1-0\sqrt{2}=1.0
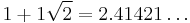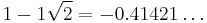1 1%2B1\sqrt{2}=2.41421\ldots 1-1\sqrt{2}=-0.41421\ldots
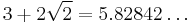2 3%2B2\sqrt{2}=5.82842\ldots 3-2\sqrt{2}=0.17157\ldots
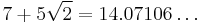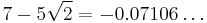3 7%2B5\sqrt{2}=14.07106\ldots 7-5\sqrt{2}=-0.07106\ldots
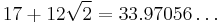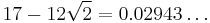4 17%2B12\sqrt{2}=33.97056\ldots 17-12\sqrt{2}=0.02943\ldots
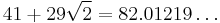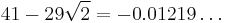5 41%2B29\sqrt{2}=82.01219\ldots 41-29\sqrt{2}=-0.01219\ldots
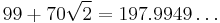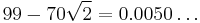6 99%2B70\sqrt{2}=197.9949\ldots 99-70\sqrt{2}=0.0050\ldots
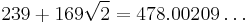7 239%2B169\sqrt{2}=478.00209\ldots 239-169\sqrt{2}=-0.00209\ldots
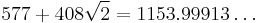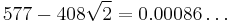8 577%2B408\sqrt{2}=1153.99913\ldots 577-408\sqrt{2}=0.00086\ldots
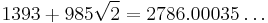9 1393%2B985\sqrt{2}=2786.00035\ldots 1393-985\sqrt{2}=-0.00035\ldots
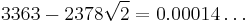10 3363%2B2378\sqrt{2}=6725.99985\ldots 3363-2378\sqrt{2}=0.00014\ldots
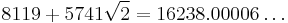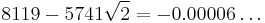11 8119%2B5741\sqrt{2}=16238.00006\ldots 8119-5741\sqrt{2}=-0.00006\ldots
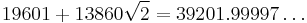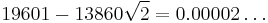12 19601%2B13860\sqrt{2}=39201.99997\ldots 19601-13860\sqrt{2}=0.00002\ldots

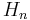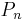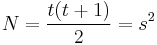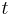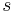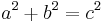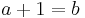The coefficients are the Half companion Pell numbers H_n and The Pell numbers P_n which are the (non-negative) solutions to H^2-2P^2=\pm1. A Square triangular number is a number N=\frac{t(t%2B1)}{2}=s^2 which is both the t\,th triangular number and the s\,th square number. A near isosceles Pythagorean triple is an integer solution to a^2%2Bb^2=c^2 where a%2B1=b.

The next table shows that splitting the odd number 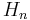H_n into nearly equal halves gives a square triangular number when n is even and a near isosceles Pythagorean triple when n is odd. All solutions arise in this manner.

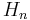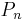n H_n P_n t t+1 s a b c
0 1 0 0 0 0
1 1 1 0 1 1
2 3 2 1 2 1
3 7 5 3 4 5
4 17 12 8 9 6
5 41 29 20 21 29
6 99 70 49 50 35
7 239 169 119 120 169
8 577 408 288 289 204
9 1393 985 696 697 985
10 3363 2378 1681 1682 1189
11 8119 5741 4059 4060 5741
12 19601 13860 9800 9801 6930

Definitions

The half companion Pell Numbers 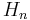H_n and the Pell numbers 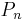P_n can be derived in a number of easily equivalent ways:

Raising to powers:

(1%2B\sqrt2)^n=H_n%2BP_n\sqrt{2}
(1-\sqrt2)^n=H_n-P_n\sqrt{2}.

From this it follows that there are closed forms:

H_n=\frac{(1%2B\sqrt2)^n%2B(1-\sqrt2)^n}{2}.

and

P_n\sqrt2=\frac{(1%2B\sqrt2)^n-(1-\sqrt2)^n}{2}.

Paired recurrences:

H_n=\begin{cases}1&\mbox{if }n=0;\\H_{n-1}%2B2P_{n-1}&\mbox{otherwise.}\end{cases}
P_n=\begin{cases}0&\mbox{if }n=0;\\H_{n-1}%2BP_{n-1}&\mbox{otherwise.}\end{cases}

and matrix formulations:

\begin{pmatrix} H_n \\ P_n \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} H_{n-1} \\ P_{n-1} \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix}^n \begin{pmatrix} 1 \\ 0 \end{pmatrix}.

So

\begin{pmatrix} H_n & 2P_n \\ P_n & H_n \end{pmatrix}= \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix}^n .

Approximations

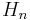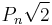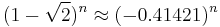The difference between H_n \, and P_n\sqrt2 is (1-\sqrt2)^n \approx (-0.41421)^n which goes rapidly to zero. So (1%2B\sqrt2)^n=H_n%2BP_n\sqrt2 is extremely close 2H_n \, .

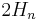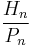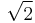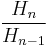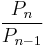From this last observation it follows that the integer ratios \frac{H_n}{P_n} rapidly approach \sqrt2 \, while \frac{H_n}{H_{n-1}}\, and \frac{P_n}{P_{n-1}}\, rapidly approach 1%2B\sqrt2 \, .

H2 − 2P2 = ±1

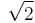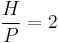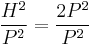Since \sqrt2 is irrational, we can't have \frac{H}{P}=2\, i.e. \frac{H^2}{P^2}=\frac{2P^2}{P^2}\, . The best we can achieve is either 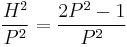\frac{H^2}{P^2}=\frac{2P^2-1}{P^2}\, or \frac{H^2}{P^2}=\frac{2P^2%2B1}{P^2} .

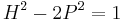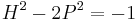The (non-negative) solutions to H^2-2P^2=1 \, are exactly the pairs H_n,P_n \mbox{ with } n\, even and the solutions to H^2-2P^2=-1 \, are exactly the pairs H_n,P_n \mbox{ with } n \, odd. To see this, note first that

H_{n%2B1}^2-2P_{n%2B1}^2=(H_n%2B2P_n)^2-2(H_n%2BP_n)^2=-(H_n^2-2P_n^2) \,

so that these differences, starting with 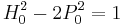H_{0}^2-2P_{0}^2=1 \, are alternately 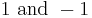1 \mbox{ and }-1 \,. Then note that every positive solution comes in this way from a solution with smaller integers since 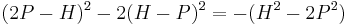(2P-H)^2-2(H-P)^2=-(H^2-2P^2) \,. The smaller solution also has positive integers with the one exception H=P=1 \, which comes from H_0=1 \mbox{ and }P_0=0 \,.

Square triangular numbers

Main article: Square triangular number

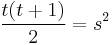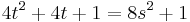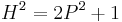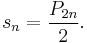
The required equation \frac{t(t%2B1)}{2}=s^2\, is equivalent to 4t^2%2B4t%2B1=8s^2%2B1 \, which becomes H^2=2P^2%2B1 with the substitutions H=2t%2B1 \mbox{ and } P=2s . Hence the nth solution is t_n=\frac{H_{2n}-1}{2} and s_n=\frac{P_{2n}}{2}.

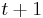Observe that t and t%2B1 are relatively prime so that 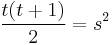\frac{t(t%2B1)}{2}=s^2\, happens exactly when they are adjacent integers, one a square 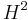H^2 and the other twice a square 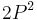2P^2. Since we know all solutions of that equation, we also have

t_n=\begin{cases}2P_n^2&\mbox{if }n\mbox{ is even};\\H_{n}^2&\mbox{if }n\mbox{ is odd.}\end{cases}

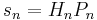
and s_n=H_nP_n\,

This alternate expression is seen in the next table.

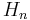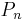n H_n P_n t t+1 s a b c
0 1 0
1 1 1 1 2 1 1 0 1
2 3 2 8 9 6 3 4 5
3 7 5 49 50 35 21 20 29
4 17 12 288 289 204 119 120 169
5 41 29 1681 1682 1189 697 696 985
6 99 70 9800 9801 6930 4059 4060 5741

Pythagorean triples

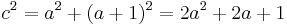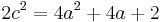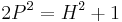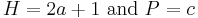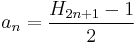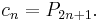
The equality c^2=a^2%2B(a%2B1)^2=2a^2%2B2a%2B1 occurs exactly when 2c^2=4a^2%2B4a%2B2 which becomes 2P^2=H^2%2B1 with the substitutions H=2a%2B1 \mbox{ and } P=c . Hence the nth solution is a_n=\frac{H_{2n%2B1}-1}{2} and c_n={P_{2n%2B1}}. \,

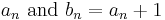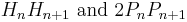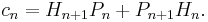
The table above shows that, in one order or the other, a_n\mbox{ and }b_n=a_n%2B1 are H_nH_{n%2B1}\mbox{ and }2P_nP_{n%2B1} while c_n=H_{n%2B1}P_n%2BP_{n%2B1}H_n.

Notes

  1. ^ For instance, Sellers (2002) proves that the number of perfect matchings in the Cartesian product of a path graph and the graph K4-e can be calculated as the product of a Pell number with the corresponding Fibonacci number.
  2. ^ For the matrix formula and its consequences see Ercolano (1979) and Kilic and Tasci (2005). Additional identities for the Pell numbers are listed by Horadam (1971) and Bicknell (1975).
  3. ^ As recorded in the Shulba Sutras; see e.g. Dutka (1986), who cites Thibaut (1875) for this information.
  4. ^ See Knorr (1976) for the fifth century date, which matches Proclus' claim that the side and diameter numbers were discovered by the Pythagoreans. For more detailed exploration of later Greek knowledge of these numbers see Thompson (1929), Vedova (1951), Ridenhour (1986), Knorr (1998), and Filep (1999).
  5. ^ For instance, as several of the references from the previous note observe, in Plato's Republic there is a reference to the "rational diameter of 5", by which Plato means 7, the numerator of the approximation 7/5 of which 5 is the denominator.
  6. ^ Pethő (1992); Cohn (1996). Although the Fibonacci numbers are defined by a very similar recurrence to the Pell numbers, Cohn writes that an analogous result for the Fibonacci numbers seems much more difficult to prove. (However, this was proven in 2006 by Bugeaud et al.)
  7. ^ Sesskin (1962). See the square triangular number article for a more detailed derivation.

References

External links